Research Papers Summary | Advances In OS Design

The write up summarises the following four research papers in the domain of Operating System design. The papers pertain to the initial advancements in the operating system design comprising of fields - thread management, thread creation, and scheduling across single and multiprocessor CPUs.

• Using Continuations to Implement Thread Management and Communication in Operating Systems, SOSO ‘91.
• Scheduler Activations: Effective Kernel Support for the User-Level Management of Parallelism, ACM Transactions on Computer Systems ‘92.
• Scheduling and Page Migration for Multiprocessor Compute Servers, ASPLOS VI ‘‘94.
• CPU Reservations and Time Constraints: Efficient, Predictable Scheduling of Independent Activities, Proceedings of the sixteenth ACM symposium on Operating systems ‘97.

Using Continuations to Implement Thread Management and Communication in Operating Systems

There were two ways that OS Kernels were handling control flows: the process model and the interrupt model. In the process model, each thread gets a separate stack in the kernel’s address space that lives for the entire life of the kernel thread, and in the interrupt model, there is a single stack per processor in the kernel space - it first has to save its state and restore when rescheduled.

It is very tempting to outrightly consider the interrupt model to be better as the saving of space is multi folds compared to the process model; however, the interrupt model is not friendly to work with as for every blocking process, a separate interrupt code will be required and this is impractical when aiming to be hardware agnostic and work independently of the underlying processor architecture. The process model also has two underlying problems; it takes up a large amount of memory and is stored in the kernel space implying machine-dependent representation, making high-level analysis infeasible. While the process model is not an issue for the likes of Accent kernel that use microcode coupled with the underlying microprocessor architecture, it is inefficient for kernels like Mach - aimed to be architecture agnostic and support multiprocessor systems.

The researchers strike a balance between the interrupt model and the process model by using continuations. Continuations, having been used erstwhile in programming languages only, provide services with the flexibility to decide how they want to come out of a “break” and what all data do they want to store when going into the “break”. The continuation architecture can be leveraged by:

• transfer that occurs at the user/kernel boundary
• thread control transfer within the kernel

The services are free to use either the process model or the continuation model - retaining the backward compatibility. The paper provides an easy to implement step by side guide on converting existing terminal services to use (or not use) continuations.

Using machine-independent context storage, continuations allow portability and high-level analysis of the stored context by other threads (leading to advantages such as stack handoff) increasing the scope of run-time optimizations like discarding stack and handing of the stack to another process requiring the data.

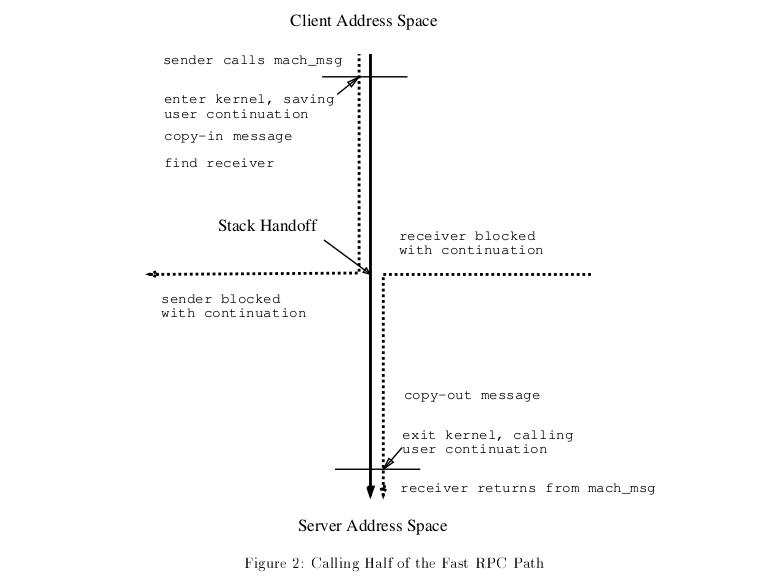
Scheduler Activations: Effective Kernel Support for the User-Level Management of Parallelism

The paper by Anderson et al. presents a new paradigm of user-managed threads which combines both a kernel interface and a user-level thread package working in cohesion.

Firstly the paper describes the current state of the threading world where any threading systems can be divided into two types: kernel-level and user-level.

The kernel-level scheme suffers from performance problems but does not exhibit scheduling and resource issues that are inherent in user-level threads. The strictly-user-level threads perform much better but operate in isolation from the underlying kernel. This often leads to problems, such as runnable threads which are idle while another thread may be blocked waiting for a resource, or lack of awareness of thread priorities. It is difficult for the user-level threads and kernel to co-exist optimally without a better communication mechanism.

The paper proposes a hybrid solution to overcome this problem, in which threads run at the user level but with significant support from the kernel. The abstraction provided to the threads package is a virtual multiprocessor whereby each process sees which processors in the system have been allocated to it. The processors allocated to any user-space process can change dynamically over time as the kernel sees fit. Scheduler activations or upcalls are essentially messages between the kernel and the user-level thread package. This communication mechanism enables the kernel to announce to the user space application information like which processor is idle or if a thread belonging to the process had been preempted. Conversely, the user-level thread library can communicate to the kernel if the process wants more processors or if one of the processors assigned to it is now idle. Via these two communication paths, a robust system of coordination can be supported.

The user-level thread library is free to use the kernel messages as it sees fit. For example, it could decide to switch running threads in light of a processor being preempted, based on relative thread priority. The whole concept exposes more control paths for both the kernel and the user; which is quite a novel idea.

The main drawback is that the upcalls are not free, and doing too many of them will defeat the purpose of such a system. However, these upcalls are kept to a minimum and only done for specific events.

SCHEDULING AND PAGE MIGRATION FOR MULTIPROCESSOR COMPUTE SERVERS

Cache-coherent shared-memory multiprocessors are scalable and offer a very tight coupling between the processing resources, which have been very attractive for use as computer servers. However one of the biggest challenges for such machines is Process scheduling and memory management, due to the distributed main memory found on them. So the paper evaluates the effects of OS scheduling and page migration policies on the performance of such servers.

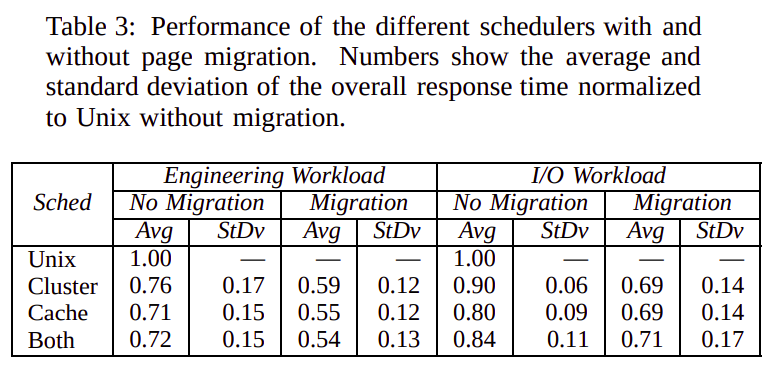
The paper’s results for workloads consisting of sequential applications show that affinity scheduling combined with a simple page migration policy improves the performance of individual applications by as much as a factor of two over the standard Unix scheduler. The evaluation was done on a sequential workload that contained a mix of both short and long-running jobs that one might encounter in a computing server environment. The sequential workload was done with cache and cluster affinity algorithms, which were then improved by adding a Page Replacement algorithm to it.

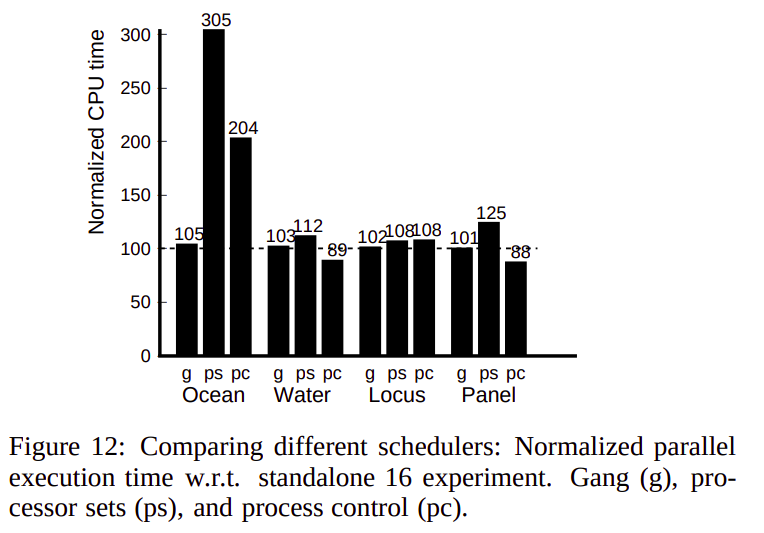
The results for parallel applications show that while the more specialized time-slicing and space-partitioning policies outperform the generic UNIX policy, there is no clear winner among them. The winning policy appears to be application-specific and depends on the importance of data distribution. Applications, where memory locality is important to perform quite well in gang scheduling due to the data locality optimizations and the Process control method, was able to give very good results in some cases due to the operation point effect.

Finally, page migration for parallel applications indicates that it may be able to use TLB-misses instead of cache-misses for implementing such policies on real multiprocessors and useful for addressing the data distribution problems of space-sharing schedulers. Different trace-based evaluation on TLB misses showed that the correlation between the page migration policy based on cache misses and TLB misses is very high, giving very good accuracy in identifying the candidate page for migration, deciding when to migrate, and also the new location to migrate to. Page migration can therefore potentially benefit space multiplexing schemes like process control where static data distribution is difficult.

The paper was able to show the evaluation of different schedulers in case of sequential and parallel workload and was also able to show that page migration policies based on TLB misses can be almost as effective as those based on perfect cache miss information.

CPU Reservations and Time Constraints: Efficient, Predictable Scheduling of Independent Activities

Personal computers are used for application with real-time workloads being executed concurrently with traditional non-real-time workloads. The paper presents such a system which does this efficiently and predictably such that:

• Activities can obtain minimum guaranteed execution rates with application-specified reservation granularities via CPU Reservations
• CPU Reservations, which are of the form “reserve X units of time out of every Y units”, provide not just an average case execution rate of X/Y over long periods, but this system will provide a stronger guarantee that from any instant of time, by Y time units later, the activity will have executed for at least X time units
• Applications can use Time Constraints to schedule tasks by deadlines, with on-time completion guaranteed for tasks with accepted constraints
• CPU scheduling overhead is bounded by a constant and is not a function of the number of schedulable tasks

The paper was implemented as the Rialto Operating System at Microsoft Research. The goal of Rialto was to bridge the gap between real-time and non-real-time applications. The research presents the idea of Precomputed Scheduling Graph both to implement CPU Reservations with application-defined periods and to implement guaranteed Time Constraints with accurate apriori feasibility analysis.

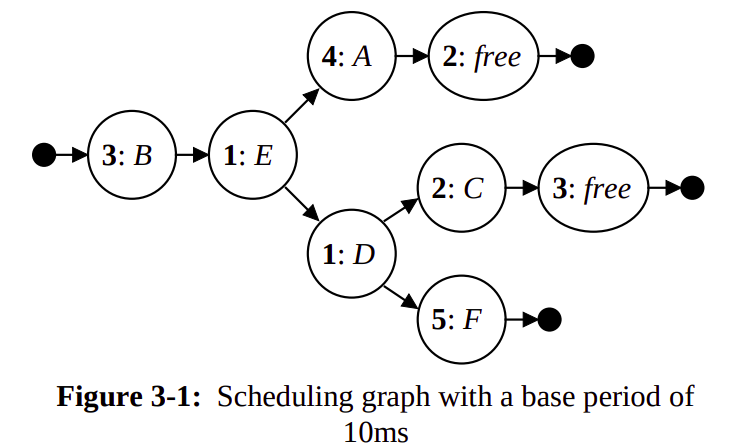
Rialto’s design allows multiple independent applications to execute concurrently, providing predictable scheduling for real-time applications even though supporting factors/resources are unknown and may change during execution.

CPU reservations are enforced with essentially no additional run-time scheduling overhead. The scheduling decision involves only a small number of pointer indirections, which is constant and independent of the number of threads, activities, and time constraints. Threads within an activity with no active time constraints execute in a round-robin fashion. Rialto is designed such that the spare CPU time is fairly shared among processes.

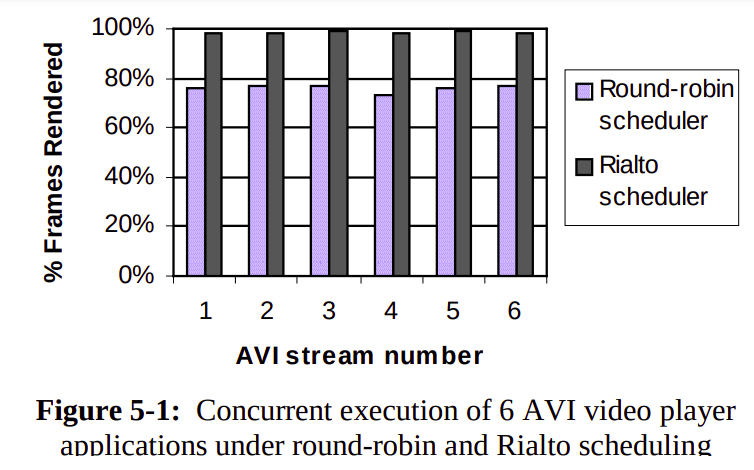
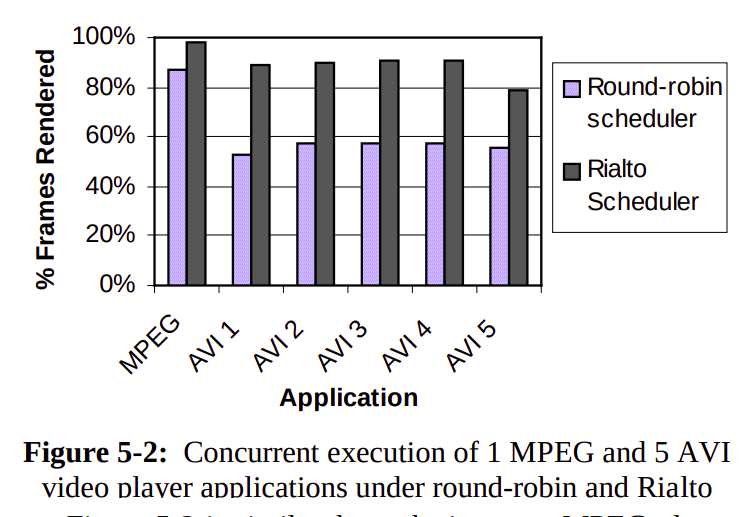
Rialto is then compared with round-robin scheduling, and the results achieved are shown in the figure. The results clearly show significant improvement by running the application and kernel (which reads incoming network packets) with appropriate CPU reservations.

Critical Considerations & Conclusion

Across all the papers, a common approach is towards delivering high-level abstractions to facilitate ease of programming and interaction by developers driven by motivations to not only apply fixes to existing architecture but open “easy” doors for further enhancements. Continuations facilitate machine independence that improves practicality and the scope of a high-level analysis to incorporate application-specific optimizations. On a similar note, the idea of abstracting virtual processor to the user-level thread packages is ingenious, granting the freedom to use different concurrency models for a user-level thread.

We realize that integration of the proposed scheduling algorithm for independent activities with general-purpose and commercial OSes leads to a question: how efficient the algorithm can be with utilizing and integrating various approaches like scheduling free and unused time like legacy scheduling algorithms. With understanding the shortcomings of existing scheduling algorithms when applied to multiprocessor architectures, a shortcoming of Rialto’s work could be scheduling symmetric multiprocessors. The issue can be addressed by generating a scheduling graph per processor but that would leave out the scope to integrate SMP scheduling policies like gang scheduling and cache affinity, possibly on a per-activity basis.

The growing complexity of scheduling algorithms, page migration techniques, and their variance across different OSes and architectures makes it harder (with every new hardware advancement) to implement continuations as apprehending (and handling) all possible “break” scenarios is near impossible. This introduced fragility is aggravated by the temptation to use continuations because of better performance with high-level abstractions. The amount of study done on the efficacy of amalgamation of the approaches is comparatively less, especially in the execution of a parallel workload where the abstractions may become a bottleneck.

Footnotes

The above work is combined efforts of the following individuals in the order of their papers as stated at the beginning of the write up:

• Shivam Kumar Jha (17CS30033)
• Prashant Ramnani (17CS10038)
• Rithin Manoj (17CS10043)
• Satyam Porwal (17CS10048)